| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 메가스캔
- 게임제작
- 노말맵
- 공부
- fbx 보안
- 손맵
- Colorize
- 메가스캔 유료화
- 레퍼런스 프로그램
- 3d 모델링 ai
- 3D AI
- 모작
- 엔진심화
- 셰이더그래프
- 프로젝트
- 배경모델링
- fbx
- normal map
- 컬러라이즈
- 재질
- pureref
- 방학셰이더스터디
- fbx 안열림
- 유니티
- 3d 뷰어
- 검색 프로그램
- 3d 모델을 로드할 수 없음
- rodin ai
- 모델링 ai
- 게임개발
- Today
- Total
베개발
02. 유니티 셰이더그래프 본문
저번시간에 이어 게시물을 작성하게 되었습니다.
목차
1. 저번시간에 배운 노드 복습 (add, multiply, split, combine, one minus)
+Color 노드
2. '회색'의 더하기와 감마 이슈
- 회색들을 더해보자
- 베버의 법칙
- 정확한 회색?
- Gamma와 Linear
- 다시 문제로 돌아가서
3. 블랙보드 활용하기
4. Lerp
5. Sample Texture 2D
5. 예제로 연습해보기
- 텍스쳐를 흑백으로 만들기
- 텍스쳐 채도를 조정하는 기능 만들기
- 텍스쳐의 밝기를 조정하는 기능 만들기
- 응용해보기
1. 저번시간에 배운 노드 복습
저번시간 마지막쯤에 노드를 몇 가지 배웠습니다.
천천히 복습해봅시다.
이미지를 보고 어떻게 계산이 이루어지는지 생각해보는 식으로 차근차근 되새김질하는 방식으로 하면 좋을 것 같네요.

계산은 기본적으로 위처럼 R,G,B값(+A값)이 각각 자리별로 계산되어 결과를 나타내게 되는 방식이었습니다. 이 점만 기억하고 있다면 이해하는 데엔 어려움이 없을 것입니다.
[Add 노드]

(1,1,0)+(0,0,0.5)=(1,1,0.5)
[Multiply 노드]

(1,0,0)*(0,0,1)=(0,0,0)
[Split, Combine 노드]

(1,0,0) → (X→R만 추출, 1) → R에 넣기
(0,1,0) → (Y→G만 추출, 1) → G에 넣기
결과값: (1,1,0)

(1,0,0) → (X→R만 추출, 1) → R에 넣기
(0,1,0) → (Y→G만 추출, 1) → B에 넣기
결과값: (1,0,1)
[one minus 노드 (반전 노드)]

1(1,1,1과 같은 뜻)-(1,0,0)=(0,1,1), 결과적으로 반전시킨 것
[+Color 노드]
다음 설명으로 넘어가기 전에 추가적으로 설명드릴 노드가 있습니다.
Color 노드입니다.
이름에서 알 수 있듯이 직관적으로 색을 넣을 수 있게끔 해주는 노드입니다. 포토샵 같은 곳에서 많이 봤던 컬러 그라데이션들에서 색을 고를 수 있습니다.

Vector4의 형태로 출력되고, 각각 R,G,B,A 채널에 해당합니다.
밑부분에 모드를 고르는 곳에서는 기본 설정으로 할 건지, HDR 설정으로 할 건지를 고를 수 있습니다.

노드 가운데에 색상이 표시되는 곳을 눌러주시고 생성되는 컬러피커에서,
이런식으로 컬러를 쉽게 골라주시면 됩니다.
2. '회색'의 더하기와 감마 이슈
새로운 노드를 배우기 전에 잠깐 짚고 넘어갈 것이 있습니다.
바로 감마 이슈에 관한 것인데요.
이 개념은 지금 배우는 것들에서뿐만 아니라 다양한 곳에서 중요한 개념으로 사용되니,
배운 것을 활용한 간단한 실험을 통해 차근차근 설명해드리도록 하겠습니다.
회색들을 더해보자
우선 '회색' 들을 add 노드를 이용해서 더하기 계산을 시켜보겠습니다.
(*여기서 말하는 회색이란 흰색과 검정색의 정가운데, 즉 정확한 회색을 지칭하는 것입니다.)
먼저 지금은 Vector4의 형태로 직접 숫자를 입력해서 더해보겠습니다.

공부했던 그대로의 결과입니다.
(0.5,0.5,0.5)+(0.5,0.5,0.5)=(1,1,1) 이니, 예상했던대로의 결과가 나왔습니다.
이걸 Color 노드에서도 똑같이 계산해보면 어떻게 될까요?
위에서 본 것처럼 그대로 (1,1,1)의 결과가 나오게 될까요?
한 번 직접 해봅시다.
Color 노드를 추가해주시고, 하단에 노란색으로 표시된 부분을 눌러 RGB 0-1.0 모드로 변경해주세요.

그런 뒤 (0.5,0.5,0.5) 의 '정확한 회색' 을 만들어 준 뒤,
해당 Color노드를 복사해 두 개의 회색 Color 노드를 준비해줍니다.
그런 다음 Add 노드로 그 두 노드들을 더해주세요.

뭔가 이상하지 않나요.
예상대로라면 흰색이라는 결과가 나와야 하는데, 회색이 나왔습니다.
이런 현상이 왜 생기는지 알기 위해서는 먼저 '베버의 법칙', 그리고 '감마 파이프라인(Gamma Pipeline)'과 '리니어 파이프라인(Linear Pipeline)' 에 대한 이해가 필요합니다.
우선 이 영상을 보시면 이해가 훨씬 쉬우실 듯 해서 첨부해놓습니다.
베버의 법칙
조용한 도서관에서 누군가 의자를 끌면 우리는 그 소리에 순간적으로 집중하게 됩니다.
하지만 시끄러운 식당에서 누군가 의자를 끌어도, 도서관에서 그랬던 것처럼 그 소리가 예민하게 들려오지는 않죠.
사람은 이처럼 '자극이 없는 상황에서 추가된 작은 자극'은 민감하게 느끼면서, '이미 많은 자극이 있는 상태에서 추가되는 자극' 은 둔감하게 느낍니다.
(사실 이런 현상들은 생존에 유리하기 위해 진화해 온 흔적입니다. 어두운 곳에서 자극을 잘 느낄 수 있다면 어두운 곳에서 생존하는 것이 유리하겠죠.
비슷하게 저번 시간에 인간이 초록색에 더 민감하다는 이야기를 했었는데, 이것은 자연의 색인 초록색에 민감하게 반응할 수 있어야 생존에 유리하기 때문이라는 것을 추측해볼 수 있습니다.)
'자극이 없는 상황에서 추가된 작은 자극'은 민감하게 느끼면서, '이미 많은 자극이 있는 상태에서 추가되는 자극' 은 둔감하게 느끼는 이 현상을 '베버의 법칙' 이라고 하며, 이 법칙은 청각, 시각 등 예외없이 모든 자극에 공통적으로 적용됩니다.
정확한 회색?
아래 두 가지의 그라데이션을 비교해봅시다.

둘 중 어느 그라데이션이 자연스러운 그라데이션, 즉 '전체적인 색의 분포가 좀 더 고르게 되어있는 그라데이션'으로 보이시나요?
첫 번째 그라데이션은 밝은 쪽으로 치우쳐져 있는 반면, 두 번째 그라데이션은 어두움과 밝음이 전체적으로 고르게 분포되어있는 것 같이 느껴지지 않나요?

각각의 그라데이션에서, 위에서 언급했었던 정가운데의 '정확한 회색'을 각각 추출해보겠습니다.

RGB를 각각 0~255 값으로 봤을 때, 위의 그라데이션은 약 187의 값이 정가운데지만, 아래의 그라데이션은 약 128의 값이 정가운데에 있습니다.
이 둘 중에서 우리가 아는 '진짜 회색' 은 어느 회색일까요?
쉽게 알아보는 법이 있습니다.
저번 시간에 디더링(병치 혼합)에 대해서 말씀드렸는데요. 점묘화가 기억나시나요?
그 방식을 이용해서 검정색과 흰색을 번갈아가며 무수히 찍게 된다면, 결국 둘이 섞여서 검정과 흰색의 중간색, 즉 회색이 나타나게 됩니다. 이런 식으로 계속 반복하면 말이죠.

그렇게 계속 반복해서 하나의 큰 이미지를 만들고, 그 옆에 128의 회색과 187의 회색을 올려보시면 이렇게 됩니다.

*이 부분은 직접 해보셔야 결과가 더 정확합니다. 이미지를 대신 만들어서 올려드렸을 땐 압축되어 올라가기 때문에 체스판무늬 부분의 색이 정확하지 않게 나오기 때문입니다.
직접 체스판무늬를 만들어보시고, 그게 모니터에 정확하게 나오게 하신 다음, 옆에 187과 128을 올리고 실눈을 떠서 어떤 색이 '진짜 회색'인지 직접 느껴보세요.
결과적으로 진짜 회색은 우리가 자연스럽다고 느꼈던 그라데이션의 128 회색이 아닌, 부자연스럽다고 느꼈던 그라데이션의 187 회색이었습니다.

즉, 우리가 자연스럽다고 느꼈던 이 그라데이션은 '수치적으로는 비선형(그래프로 치자면, 대각선으로 반듯이 올라가는 모양이 아님)이다' 라고 말할 수 있습니다.
이 그라데이션을 그래프로 표현해보자면 이렇습니다.
(0~255를 0~1로 표현한 것입니다.)

(출처:https://www.mathway.com/ko/Trigonometry)
일직선이 아닙니다. 즉 비선형입니다.
위에서 설명드린 '베버의 법칙' 을 기억하시나요?
사람은 어두운 부분에서의 변화를 더 민감하게 받아들이고, 그렇지 않은 부분에서의 변화는 덜 민감하게 받아들인다는 내용이었는데요.

이 '자연스럽지 않은' 그라데이션은, 위에서 말한 우리가 자연스럽게 느끼는 그라데이션과는 다르게 사실 0부터 255까지 차근차근, 한단계씩 올라가고 있는 상태(이를 선형적(linear)이라고 합니다.)였으나, 우리는 베버의 법칙에 의해 밝은 부분에서의 변화는 잘 눈치채지 못하므로 전체적으로 밝은 부분이 더 넓게 분포해있다고 느끼게 되었던 것입니다.
이 그라데이션을 그래프로 나타내면 다음과 같이 됩니다.

선형적(linear)입니다.
그래서 '컴퓨터는 어두운 부분의 정보를 좀 더 세밀하게 저장하기 위해, 전체적으로 0.45승을 해줘서 밝게 만들어 저장했다가, 모니터에 출력할땐 모니터 자체에서 2.2승을 해줘서 다시 어둡게 만들어주는 과정을 거치게 됩니다.'
밑줄 친 부분을 예시 이미지와 함께 좀 더 보기 쉽게 정리해보았습니다.
(예시 이미지는 제가 했던 과제입니다. ㅎㅎ)

두 그래프에 관해 설명하자면 다음과 같습니다.

이 과정은 주어진 비트 수 내에서, 밝은 쪽에 할당되는 비트의 양을 좀 더 인간이 인식하기 쉬운 어두운 영역으로 할당하여, 이미지를 최적의 품질로 보여주기 위해 일어나는 과정입니다.
Gamma와 Linear
그런 과정들이 모니터에서 인간 모르게 일어나는데, 이제 게임 엔진으로 들어가면서 이러한 감마 연산과 아까 우리가 했던 add 등의 연산이 같이 일어나게 되면서 문제가 생기게 됩니다.
현재의 유니티에는 감마 파이프라인과 리니어 파이프라인 이렇게 두 가지가 존재합니다.
하지만 유니티 버전 3.5 미만에서는 감마 파이프라인밖에 존재하지 않았습니다.
이때는 색의 연산이, 색이 srgb로 계산되어 밝아진 상태에서 그 상태로 계산을 하기 때문에,

계산을 끝낸 시점에서 이미 사라진 밝은쪽의 정보들이 손실되기 때문에 다시 모니터에 출력되었을때 하얗게 날아가는 부분이 생기게 된다는 것입니다.
하지만 리니어 파이프라인에서 계산을 진행하게 된다면,

(이미지는 클릭하시면 크게 보입니다.)
우선 색이 srgb로 계산되어 밝아진 상태로 저장됐다가, 계산이 진행되기 전 다시 모니터에 출력되는 그 상태로 어둡게 감마 보정을 해주고(심지어 지원되는 하드웨어에서는 이 작업이 공짜라고 합니다.), 그 상태에서 계산을 하기 때문에 밝은 쪽의 정보들이 손실되지 않은 상태에서 srgb로 저장을 해주고, 다시 모니터에 감마보정을 해서 출력해주기때문에 날아가는 부분이 생기지 않은 채로 좀 더 정확하게 표현을 해주게 됩니다.
아래는 유니티 매뉴얼의 감마 파이프라인과 리니어 파이프라인 비교 이미지입니다.
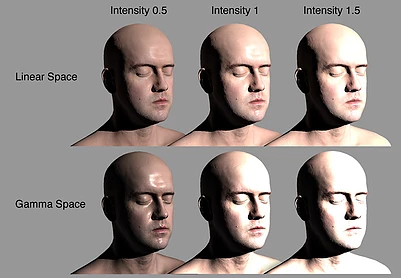
(출처:https://docs.unity3d.com/Manual/LinearRendering-LinearOrGammaWorkflow.html)
확실히 감마 파이프라인일 때, 색이 더 하얗게 날아가는 것을 볼 수 있습니다.
그래서, linear 파이프라인으로 진행하는 것이 훨씬 더 보기에 좋습니다. 예를 들어 이펙트 같은 경우에도 add를 자주 쓰고, 밝아지는 일이 흔하기도 하니 linear파이프라인으로 진행하는 것이 좋겠습니다.
다시 처음에 생긴 문제로 돌아가봅시다.

그렇다면, 이 이미지에서 우리가 더 자연스럽게 느꼈던 아래쪽 그라데이션은 위의 리니어 그라데이션에서 감마 보정이 2.2 들어간 상태라고 할 수 있을 것입니다. (실제로 0~255에서의 187과 128을 각각 0~1에서의 퍼센트로 바꿔 계산해보면 같은 결과가 나옵니다.)
또한 비선형적이라고도 말할 수 있습니다.
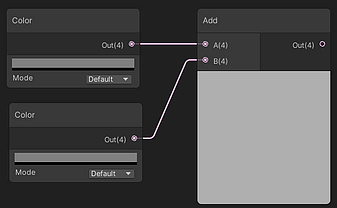
처음에 문제가 발생했던 Color 노드에서 우리가 골랐던 (0.5,0.5,0.5) 의 회색은 사실, 리니어 상태에서의 중간값을 고르려고 했던 우리의 의도와는 달리
이미 감마 보정이 들어간 상태의 회색으로, 리니어 컬러로 정확히 따지면 (0.21,0.21,0.21)에 가깝습니다.(0.5의 2.2승입니다.)

유니티에서는 Color 노드를 텍스쳐와 같이 리니어 공간이 아닌 srgb공간에서 관리하기 때문에, 감마 보정이 들어가 실제보다 어두워질수밖에 없습니다. 즉 Color 노드에서 색을 고르면 리니어 컬러와 같은 상태로 색이 표현되지 않는다는 뜻입니다.
이런 현상을 해결해주기 위해서는 Colorspace Conversion이라는 노드를 활용하면 됩니다.
이 노드는 리니어 컬러를 rgb컬러(감마 보정이 들어간 컬러)로 바꿔주거나, 혹은 그 반대의 작업을 수행할 수 있습니다.

Color 노드의 감마 보정된 것을 제거해서 리니어 컬러로 변환시키려면, Colorspace Conversion 노드를 다음과 같이 세팅해주면 됩니다.
* 현재 (21.01.23) 기준으로 해당 노드의 설정이 반대로 되어있다고 합니다. 원래는 RGB→Linear 의 형태가 되어야, 감마 보정을 제거해준다는 것이 되는데.. 아직 수정 전이라고 합니다.
이제 이렇게 바꿔준 컬러를 더해봅시다.

깔끔하게 흰색이 나옵니다.

이렇게 밑에서 설명해드릴 Sample Texture 2D에 Colorspace Conversion 노드를 적용해서 감마 보정을 없애면, 아까 srgb공간에 저장된 이미지의 예시로 보여드렸던 것과 같이 밝아지는 것도 확인할 수 있습니다. 다만 순수한 텍스쳐는 쉐이더로 넘어올 때 다 리니어 연산을 거쳐 넘어오기 때문에, 감마 이슈가 일어나진 않기 때문에 이 부분은 고민하지 않으셔도 됩니다. 해당 이슈가 일어나는 것은 셰이더그래프 내에서 Color 노드를 생성했을 때 뿐입니다.
3. 블랙보드
본격적으로 셰이더를 만들기 전에, 좀더 작업을 편하게 해주는 기능을 알아보고 가겠습니다.
블랙보드는 유니티 셰이더그래프 내의 변수를 인스펙터 창에 노출시켜서, 사용자가 좀 더 쉽게 변수들을 통제할 수 있도록 만들어주는 일종의 인터페이스 기능입니다.

셰이더그래프를 여시면 왼쪽 상단에 보이는 것이 블랙보드입니다.

+를 눌러주시면 변수형들이 뜨게 됩니다. 우선 간단하게 Vector1을 골라보겠습니다.

그럼 이렇게 뜨게 되는데요. 간단하게 블랙보드의 기본 메뉴를 알아보겠습니다.

참고로 레퍼런스 이름 앞에 _를 붙이는 것이 프로그래머분들 입장에서 편하다고 합니다.
모드를 'Default'로 설정해두면 float값을 입력할 수 있습니다.
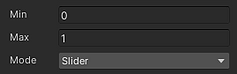
모드를 'Slider'로 설정해두면 인스펙터 창에서 슬라이드 형태로 변수를 조절할 수 있고, 슬라이더의 최소값과 최대값을 정해둘 수 있습니다.

모드를 'Integer'로 설정해두면 정수값만 입력할 수 있습니다.
-2,-1,0,1,2... 이렇게 끊겨서 설정이 됩니다.
저는 TestValue라고 이름을 붙인 Vector1 변수를 만들어보았고, 모드는 슬라이더로 설정해두었습니다.
변수명이 적힌 곳을 드래그해서 셰이더그래프에 놓으면 변수를 쉽게 꺼내올 수 있고, 그대로 셰이더의 Color에 드래그해서 연결해줍시다.

바로 TestValue의 기본값인 0이 컬러로 들어가게 되는 것을 확인할수가 있습니다.
이제 셰이더그래프 맨 왼쪽 상단의 Save Asset을 눌러서 저장해줍니다.
씬 뷰로 돌아가서 sphere를 하나 생성해주고, 방금 만든 셰이더를 적용한 머테리얼을 그 sphere에 적용시켜줍니다.

그럼 인스펙터 창에 이렇게 아까 만든 TestValue가 슬라이더 형태로 노출되어있고,

슬라이더를 움직이면 실시간으로 잘 적용됩니다.
4. Lerp
Lerp란, 'Linear Interpolation', 즉 '선형 보간' 을 말합니다.
간단히 말하자면 '두 개를 섞는다' 라는 것입니다.
좀 더 자세히 살펴보자면, 여기서 Linear라는 것은, 위에서 설명했다시피 그래프가 직선 모양으로 일정하게 증가하는 것을 의미하고,
보간이라는 것은 '사이를 보정한다' 정도의 뜻이 됩니다.
다른 노드들을 추가했던 것과 같이 우클릭 후 'lerp'를 검색해주시면 lerp 노드를 추가할 수 있습니다.
아무 색이나 두 개를 만드신 후 사진처럼 연결해주세요.
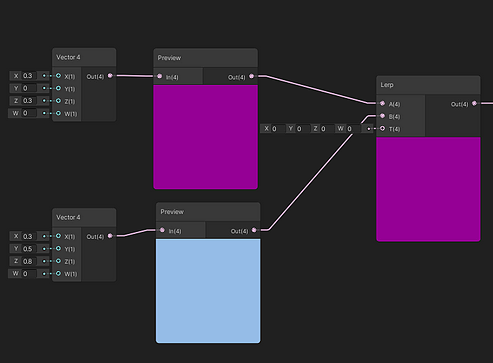
그 다음, Lerp의 맨 마지막에 있는 (사진에서 T라고 써있는곳) 노드에 Vector1 노드를 연결하고, 해당 노드를 property 로 만들어 블랙보드에 추가해주세요.

변수명은 Lerp로 하고, 사진과 같이 slider 모드로 만들어주세요.
나중에 인게임에 적용해서 확인하기 쉽게 하기 위함입니다.

좌측 최상단의 save asset을 눌러서 저장해주세요.
그 다음, 위에서 했던대로 머테리얼을 만들어서 sphere에 적용하면,

잘 작동됩니다.
슬라이더를 만들었으니 한번 만져봐야겠죠.

아까 추가했던 두 색이 슬라이더 상태에 따라서 섞여 나오는 것을 볼 수 있습니다.
이제 이게 어떤 원리로 작동하는지 알아봅시다.
직관적인 설명을 위해 (1,0,0)과 (0,1,0)을 섞어보겠습니다.

현재 lerp의 값은 0입니다. 그 결과 (1,0,0)이 나왔습니다.

lerp의 값을 1로 해주면 두 번째 색인 (0,1,0)이 나옵니다.
그렇다면 lerp의 값을 0.5로 해준다면?

뭔가 오묘한 색이 나왔습니다.
이 색은,

'(0.5,0.5,0)' 입니다.
그렇다면 만약 Lerp가 0.7이라면?


(0.3,0.7,0) 이라는 결과값이 나옵니다.
Lerp는 주어진 두 가지 색을 말 그대로 '섞어주는' 기능을 하는데요.
정확히 말하자면, 전체를 1로 보고, 우리가 입력한 비율에 맞춰(위에서는 순서대로 1,0,0.5,0.7이 그 값이었죠.) R,G,B값을 각각 계산한 뒤 결과를 내는 것입니다.
좀 더 정확히, 이걸 식으로 표현하자면,
첫번째 색을 A, 두번째 색을 B, 비율을 t라고 했을 때,
{(1-t)*A}+(t*B)
이렇게 표현됩니다. 비율을 곱해서 더해주는 것이죠.
물론 Lerp는 색 뿐만 아니라, 다른 Vector1 이나 2 같은 거의 모든것에 대해서 선형 보간을 할 수 있습니다.
다음 주제로 넘어가기 전, 텍스쳐를 Lerp 시키는 것을 보여드리겠습니다.

역시 텍스쳐도 잘 작동되네요. (귀여운 고양이)
5. Sample Texture 2D

방금 보여드린 gif를 보시면 인스펙터 쪽에 Texture2D 라는 것이 보입니다.
그렇습니다. 이미 알고계실 '텍스쳐' 입니다. 이걸 노드에서 보면,

이렇게 되어있습니다.
Input 값들을 차례대로 보면, Texture(T2), UV(2), Sampler(SS) 이렇게 3개가 있고, 그 밑에 타입과 Space 가 있습니다.
우선 간단하게 이미지로 정리해보았습니다.

Texture(T2)
지금까지 진행하시면서 눈치채셨겠지만 Input 이름 옆의 괄호 안에 써있는 것은 해당 input값의 데이터 타입입니다.

이렇듯 아까 진행했던 Lerp 노드에서도 각각 A,B,T 라는 input 값이 있었고, 그 3가지 옆에 쓰여있는 (4) 는 각각의 input이 Vector4라는 데이터 타입을 가지고 있다는 것을 의미했었습니다.
마찬가지로 Texture(T2) 의 (T2)는, 간단하게 '2차원 텍스쳐' 라는 데이터 타입을 의미합니다. 우리가 자주 보는 보통의 이미지 파일들이 대부분 2차원 텍스쳐입니다.
(대표적인 3차원 텍스쳐는 흔히 볼 수 있는 LUT 텍스쳐입니다. 나중에 다루게 될 것 같네요.)
Vector2와는 다릅니다. Vector2는 단순히 (a,b) 이렇게 두 가지 값만을 가지고 있는데 반해, 2차원 텍스쳐는 '첫 번째 픽셀에 (R1,G1,B1,A1), 두 번째 픽셀에 (R2,G2,B2,A2)...' 이런 식으로 값들을 가지고 있기 때문이죠.

다만, 셰이더그래프에 바로 이렇게 이미지를 드래그해서 넣게되면 인스펙터 창에서 수정이 불가능합니다.
저 Texture 인풋에, 이렇게

Texture 2D Asset 이라는 노드를 추가해준 뒤, property 로 만들어서


이렇게 인스펙터 창에서 바로 넣을 수 있게끔 해야 합니다.
(블랙보드에서 바로 Texture2D를 생성해도 됩니다.)
UV(2)
모델링할 때의 그 UV입니다.

간단한 큐브 모델링과 그 UV입니다.
해당 모델링에

이런 텍스쳐를 입히게 되면,

이런 결과를 얻을 수 있습니다.
여기까지는 모델링을 진행하며 많이 거쳐왔던 과정인데요. 조금 더 깊게 들어가보겠습니다.
메쉬를 이루고 있는 버텍스는 버텍스 컬러, 인덱스, 포지션, 노말, UV 등의 값들을 가지고 있습니다.

맥스에서 메쉬를 export 하게 되면, 각각의 버텍스 값들을 맥스에서 뽑아내게 되는 것이고, 엔진에 import 하면 가져온 버텍스 정보들을 하나의 입체 오브젝트로 표현해주게 되는 것입니다. 즉, 각각의 점들이 있고, 그 점에는 점들을 어떤 순서로 잇는지, 점들이 바라보는 방향은 어디인지 등의 정보가 들어있다고 생각하시면 됩니다. 위의 주사위 모델링도 그저 8개의 점들이 가지고 있는 정보들로 이루어진 오브젝트죠. 그걸 컴퓨터가 계산해서 이렇게 입체적인 모습으로 나오게 되는 것입니다.
그 오브젝트에 텍스쳐를 입히게 되면서 UV라는 정보가 필요해졌습니다.
UV는 Vector2 인것을 위에서 확인할 수 있는데요,
이 UV는, 기존의 3D 좌표에서 x,y,z 라는 3개의 축을 이용한 것과 같이, u,v라는 두 개의 연속된 알파벳을 축 이름으로 이용하기 위해 가져온 것입니다.
버텍스가 가지고 있는 (0,0) 부터 (1,1) 사이의 좌표값은 이미지의 좌표값에 대응해서,
결과적으로 '맵핑'되어 화면에 나타나게 됩니다.
이미지는 정규화(normalize) 과정을 거쳐서 (0,0)에서 (1,1) 사이의 값을 가진 2차원 좌표로 변환됩니다. 마치 0~255까지의 값을 가졌던 RGB 정보가 0에서 1 사이로 표현 되었던 것처럼!
(0%에서 100%로 대부분의 범위를 정규화해서 표현 가능하기 때문에, 이 같은 방법은 많은 곳에서 활용됩니다.)
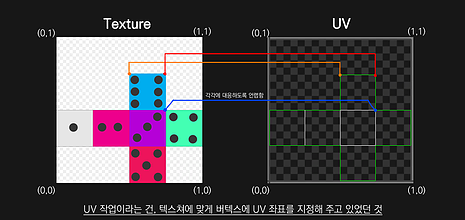
즉, 지금까지 했던 UV 언랩 작업은, '텍스쳐에 맞게 버텍스에 UV 좌표를 지정하는 작업' 을 하고 있었다는 것입니다.
이렇게 버텍스에 UV 좌표를 지정해주면, 오브젝트가 렌더링될 때 텍스쳐의 해당 UV좌표 부분을 버텍스로 찍어 가져와서 텍스쳐를 바르고, 다른 면도 똑같이 해주는 식으로 화면에 어떻게 보일지가 결정됩니다.
이 UV 좌표는 하나의 오브젝트가 여러 개를 가질수도 있습니다. 즉 UV 채널이 여러개 있다고 말합니다. 대표적으로 확인해볼 수 있는게 바로 라이트맵 UV입니다.

자동생성된 라이트맵 UV..
이렇게 라이트맵 UV가 만들어지는 경우, 원래 텍스쳐를 맵핑할 때 작업을 진행했었던 UV 채널은 그대로 둔 채, 그 다음 UV 채널에 라이트맵 UV가 만들어지게 됩니다.
이렇게 쉽게

맥스와,

유니티에서도 확인해볼 수 있습니다.
다만 맥스에서 UV채널은 1부터 시작하는 데 반해, 유니티에서는 0부터 시작하니 이 점 유의해주세요.
참고로 TexCoord = Texture Coordinate = UV 셋 다 같은 용어입니다. Texture Coordinate는 텍스쳐 좌표계라는 뜻인데, 위에서 말했던 (0,0)부터 (1,1) 까지의 공간을 의미합니다.
5. 예제로 연습해보기
공부할 땐 역시 문제를 풀어봐야 실력이 빠르게 느는 것 같습니다.
문제 답을 보기 전에 직접 풀어보시는 걸 추천드립니다.
1) 텍스쳐의 채도를 조절할 수 있는 셰이더 만들기
아래와 같이 만드시면 됩니다.

*물론 포토샵을 써 봤다면 익숙할 saturation 이라는 기능의 노드가 여기에도 있습니다. 그러나 이번 문제에서는 해당 노드를 사용하지 않고 만들어보도록 합시다.
우선 채도를 조절하기 전에, 텍스쳐를 아예 흑백으로 만들어보겠습니다.
간단하게 생각하면 r,g,b 각각을 더한 다음 3으로 나누면, rgb의 평균값이 0~1의 범위 사이에서 나오게 되겠죠.

add와 divide 노드를 이용해 그대로 만들어주었습니다.

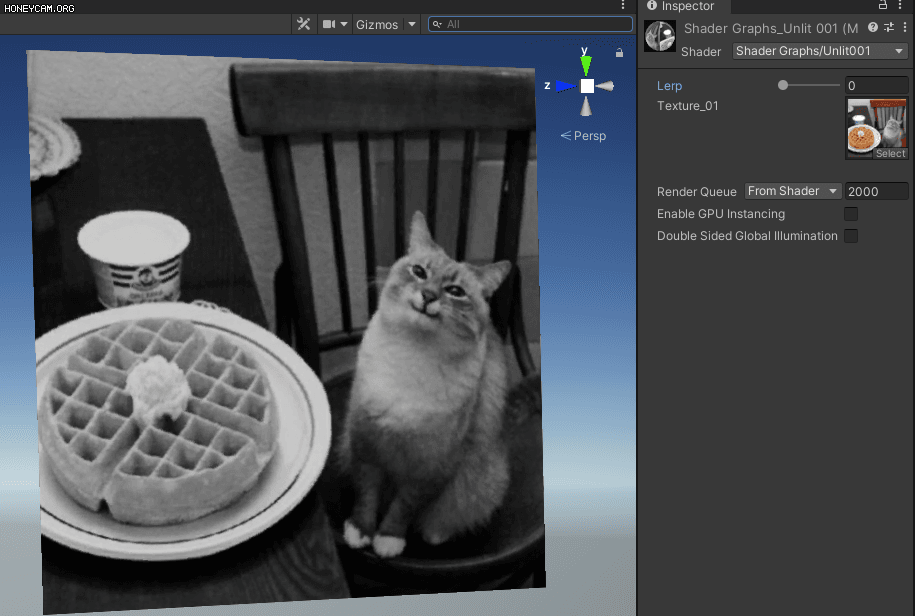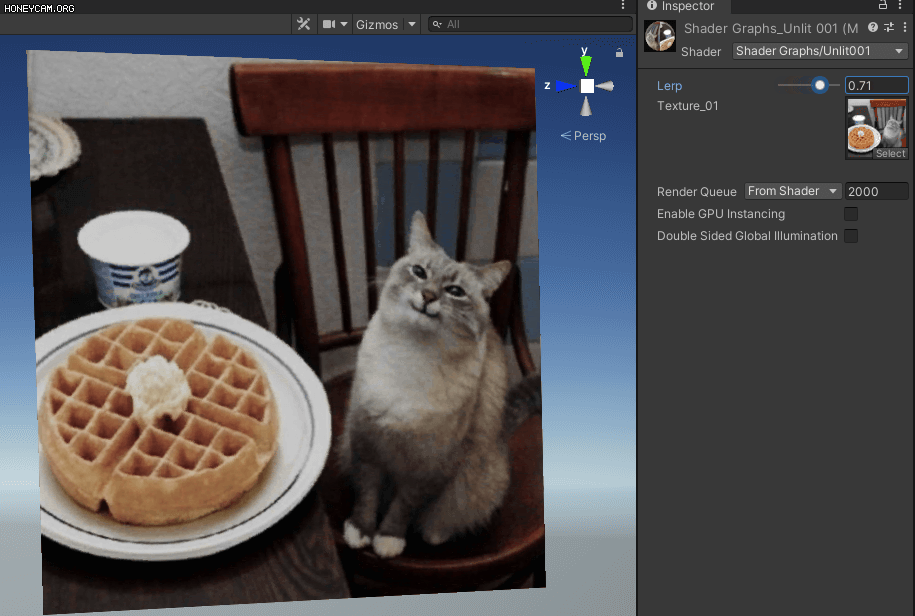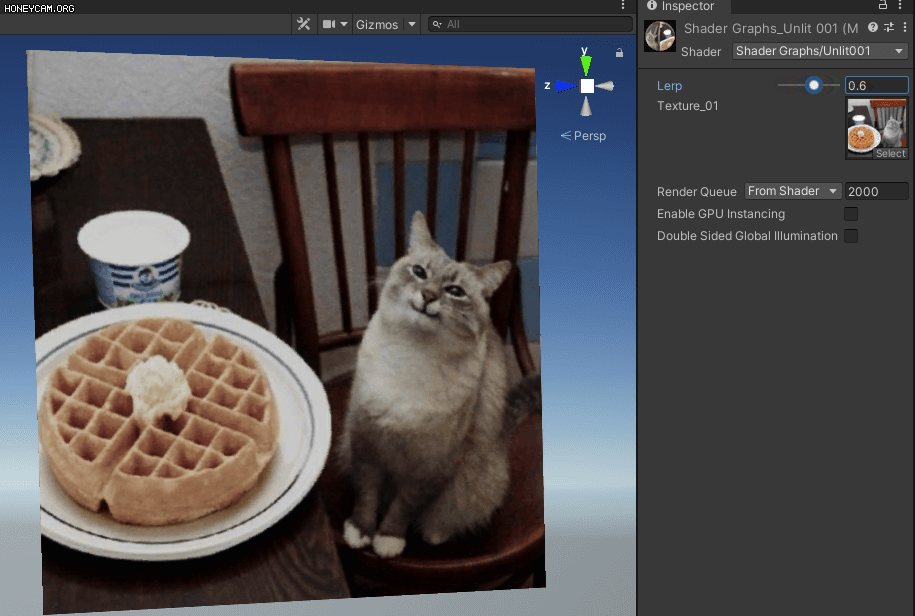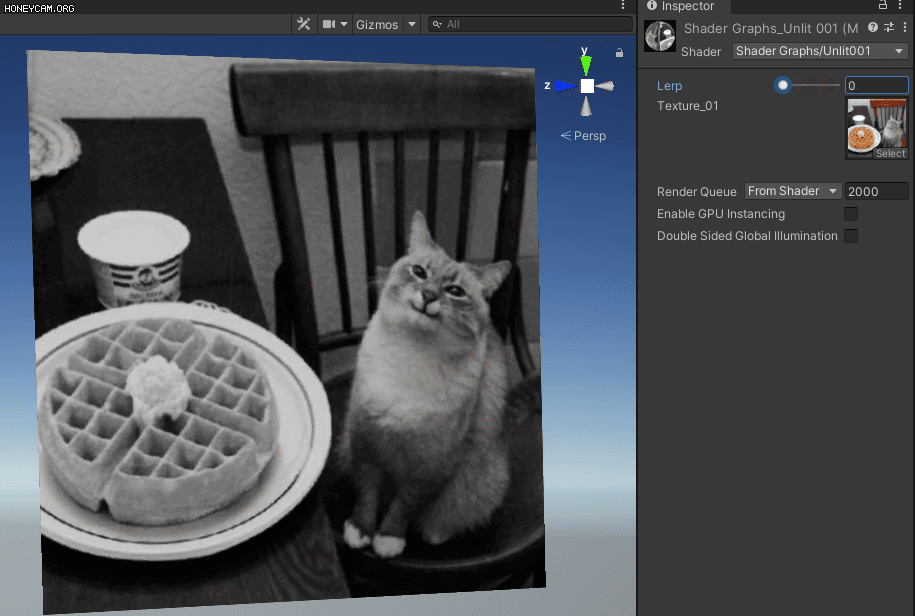
어딘가 사연있어 보이는 고양이가 되었습니다.
그 다음, 이 결과값을 원본과 Lerp 시켜 줍니다.


성공적으로 셰이더를 만들었습니다!
다만, 약간 부정확해보일 수 있는데 이건 우리 눈이 R,G,B 각각을 받아들이는 강도가 다르기 때문입니다.
좀 더 정확히 하자면 R에 0.299, G에 0.587, B에 0.114를 곱해준 뒤 더해주면 됩니다. (이미 비율로 환산해서 계산한 것이기 때문에 다시 3으로 나눠 줄 필요는 없습니다.)
G의 비중이 가장 높은 것은 저번에 언급했듯이 인간은 초록색에 가장 민감하기 때문이라고 볼 수 있겠습니다. 이를 NTSC가중치라고 부릅니다.
조금 더 정확한 결과물입니다.
2) 텍스쳐의 밝기를 조절할 수 있는 셰이더 만들기
이번엔 밝기입니다.

아마 많은 분들이 처음에 multiply를 적용하셨을 거라고 생각합니다. (저 역시 마찬가지였습니다.) 하지만 그런 방식은 텍스쳐를 어둡게 만들기만 할 뿐, 밝게는 만들지 못합니다. 이것저것 실수해보면서 감을 키우는 것도 좋은 방법입니다.
여기서는 add 노드를 이용해서 텍스쳐의 밝기를 조절합니다.
add는 '더하는'기능을 하는 노드이니 어떻게 어두워지게 하나 생각하실 수도 있지만, 이건 add 값에 음수를 넣어주면 되는 문제입니다. 음수를 더하는 건 빼기를 하는 것과 같기 때문입니다.
이렇게 노드를 연결해주고,


Add에 더해줄 Vector1 슬라이더의 범위를 -1에서 1로 만들어줍니다.

그러면 이렇게 성공적으로 밝기 조절 셰이더가 만들어집니다.
다만, 전에 HDR에 대해 말씀드린 적이 있는데, 만약 저 상태로, 픽셀 하나의 값에 (1,1,1)이 더해지게 된다면 색의 R,G,B 값은 각각 1을 넘어가서 HDR 컬러가 됩니다. 나중에 포스트 프로세싱을 적용해주는 등의 과정을 거치면 상당히 밝아보이거나 굉장히 어두워보이는 일이 생길 수 있습니다.
그런 일을 방지하기 위해서, Clamp 라는 노드를 이용해줍시다.
이 노드는 일정 범위 밖에 있는 값은 잘라내버리는 기능입니다.

이렇게 해주시면 색이 HDR 영역까지 넘어가지 않는 안정적인 셰이더가 완성됩니다.
R,G,B값과 밝기, 채도 모두 조절 가능한 셰이더

지금까지 했던 것을 모두 합해주면 됩니다. 다만 순서를 조금 유의하셔야 합니다.

-
R,G,B 각각에 -1부터 1까지 더해줄 수 있는 각각의 변수를 만들어서 add 노드로 연결해줍니다. (R,G,B 값을 각각 조절 가능하게 되었습니다.)
-
이 셋을 combine 노드로 합해줍니다.
-
아까 R,G,B값을 조절해준 결과물에 NTSC 가중치를 곱한 뒤 더해서 채도를 제어할 수 있는 노드를 만듭니다.
-
아까 2번에서 만들었던 것과 Lerp 노드로 연결해줍니다. (채도를 조절 가능하게 되었습니다.)
-
여기에 -1에서 1까지 더해줄 수 있는 노드를 추가해줍니다. (밝기를 조절 가능하게 되었습니다.)
-
추가로 Clamp 노드를 이용해 범위를 0부터 1까지로 제한해 줌으로써, 색이 HDR 영역으로 넘어가지 않게끔 만들어줍니다.
여기에서 예를 들어, 밝기 조절 기능 뒤에 Lerp로 채도를 조절하는 기능을 연결해준다면, 채도가 낮을수록 밝기 조절 기능이 먹지 않는 이상한 오류가 생깁니다. 이런 점들을 잘 생각해서 노드를 다뤄야 합니다.
가장 중요한 것은 위의 설명들을 이해하고 자신의 것으로 만들어서 응용할 수 있도록 하는 것입니다. 무작정 암기하는 것은 좋은 공부법이 아닙니다.
'대학교 공부' 카테고리의 다른 글
| [엔진심화] 01. 프리팹(Prefab)과 FBX (0) | 2021.03.29 |
|---|---|
| 2학년 1학기 카라렌 과제 - 3ds max scanline 렌더러로 재질 만들기 (0) | 2021.03.15 |
| 4. 버텍스 컬러와 활용 (0) | 2021.03.15 |
| 03. UV 응용하기 (1) | 2021.03.15 |
| 01. 색상 표현 기본원리, 색 연산 기초 (2) | 2021.03.15 |




