| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 공부
- UE5
- 메가스캔 유료화
- 3d 뷰어
- normal map
- 메가스캔
- 모작
- 프로젝트
- 3d 모델링 ai
- 노말맵
- rodin ai
- 노말맵깨짐
- 재질
- fbx 안열림
- 배경모델링
- 방학셰이더스터디
- fbx 보안
- 게임제작
- 3d 모델을 로드할 수 없음
- 유니티
- 3ds Max
- 엔진심화
- 셰이더그래프
- 스무딩그룹
- 게임개발
- 게임그래픽
- 3D
- 레퍼런스 프로그램
- 모델링 ai
- fbx
- Today
- Total
베개발
[엔진심화] 08. 함수, 좌표계, 벡터 본문
목차
- 함수
- 매개변수와 인수
- 시멘틱
- 함수의 스코프 - 좌표계
- 월드 좌표계
- 로컬 좌표계
- 좌표 공간의 종류 - 벡터
- 개념 이해
- 벡터의 덧셈
* 공부 과정에서 작성한 글이기 때문에 틀린 내용이 있을 수 있습니다.
■ 함수
함수는 정의 부분과 사용(호출) 부분으로 나눈다.
정의는 한 번만 하고 다른 곳에서 여러 번 사용되는 식으로 쓰여지는데, 정의 부분에서 함수의 리턴 값에 대한 자료형을 지정해줘야 한다. 예를 들어 해당 함수가 맨 마지막에 float형의 결과를 내놓아야 한다면 float 형이라고 직접 지정해줘야 한다는 의미이다. 단 리턴 값이 없는 함수는 void로 정의한다.
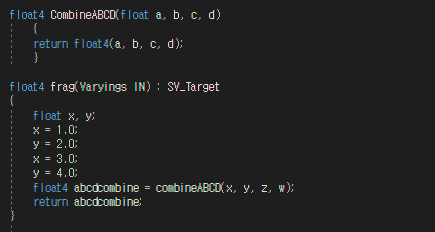
매개변수와 인수
float4 CombineABCD(float a, b, c, d)
{
return float4(a, b, c, d);
}
float4 frag(Varyings IN) : SV_Target
{
float x, y;
x = 1.0;
y = 2.0;
x = 3.0;
y = 4.0;
float4 abcdcombine = combineABCD(x, y, z, w);
return abcdcombine;
}
위 구조에서 1번째 줄의 CombineABCD 라는 함수의 a,b,c,d가 매개변수이며, 아래에 combineABCD라는 함수를 호출해둔 상태에서의 x,y,z,w가 인수이다.
매개변수와 인수의 개수, 순서, 자료형은 같아야하지만, 함수를 사용할 때의 인수명은 모두 다를 수 있다. 하나의 함수는 여러 곳에서 사용되기 때문이다.
1번째~4번째 줄에서 보이는 바와 같이 함수를 정의하는 부분에서, 매개변수명은 함수 내부에서 사용되는 이름과 같아야한다. 즉,
float4 CombineABCD(float a, b, c, d)
{
return float4(x, y, z, w); //←?? x,y,z,w가 갑자기 튀어나왔다.
}
이런 식으로 만들어지면 안 된다는 것이다.
시멘틱
프래그먼트 셰이더의 경우 각 용도에 따라서 저장되는 공간이 미리 할당되어 있는데, 이를 hlsl에서 다룰 때 특정 함수의 리턴값이 어디에 들어갈지를 미리 정해줘야 할 때 이것을 시멘틱이라고 한다.
struct Attributes
{
float4 positionOS : POSITION;
float2 uv : TEXCOORD0;
};
위에서 볼 수 있다시피 positionOS라는 변수는 위치 정보를 받아들이는 것이고, uv라는 변수는 uv 정보를 받아들이는 것이라고 미리 변수에 의미를 부여해두었다.
함수의 스코프(Scope)
우리말로 표현하자면 '유효범위' 를 뜻하는 것이다.
변수가 선언된 위치의 중괄호, 그리고 하위 중괄호까지 유효하다.
즉, 다음과 같은 구조에서
{a
{b}
{c}
}a에서 선언된 변수는 b와 c에서도 사용가능하지만, b에서 선언된 변수는 c에서는 사용하지 못한다는 의미이다.
■ 좌표계
월드 좌표계
오브젝트가 기본 상태로 있을 때는 오브젝트의 parent가 월드 자체라고 볼 수 있다.
여기 각각 파란색, 주황색인 병아리 오브젝트가 있을 때,

지금 상태에서는 각각의 parent는 존재하지 않으므로 둘 다 월드 좌표계가 로컬 좌표계와 동일하다. (기준점이 되느 ㄴ것이 월드 좌표이기 때문에)
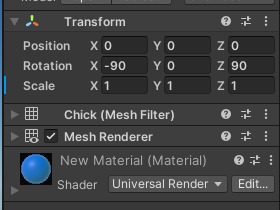
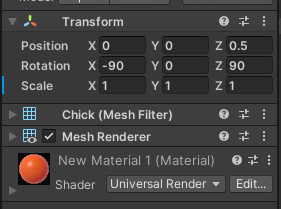
이와 같이 월드를 기준으로 했을 때 오브젝트의 좌표를 월드 좌표계라고 부른다.
로컬 좌표계
하지만 만약 주황색 병아리가 파란색 병아리 하위로 들어가게 되어서, 파란색 병아리가 주황색 병아리의 parent가 되는 구조로 변하게 되면,

주황색 병아리는 parent인 파란색 병아리를 기준점으로 해서 좌표계가 변경되므로,
사진과 같이 변하는 것을 볼 수 있다.
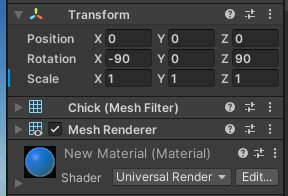
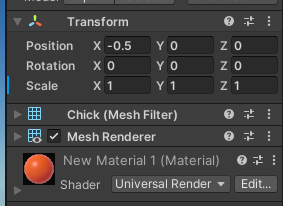
주황색의 위치가 (-0.5,0,0)으로 바뀌었는데, 이건 파란색 오브젝트를 기준점으로 봤을 때 상대적으로 x축 방향으로 -0.5만큼의 거리에 위치하고 있다는 의미이다.
이와 같이 월드가 아닌 오브젝트를 기준으로 했을 때 오브젝트의 좌표를 로컬 좌표계라고 한다.
이때 주황색 오브젝트는 '파란색 오브젝트의 공간 좌표계에 소속되었다'고 표현할 수 있다.
즉 파란색 오브젝트의 공간에 주황색 오브젝트가 들어갔다는 의미와 같다.
이럴 경우, 만약 상위 오브젝트인 파란색 오브젝트를 이동시키거나 회전시켰을 때, 하위 오브젝트인 주황색 오브젝트의 좌표에는 변화가 없다.
왜냐하면 파란색 오브젝트 자체는 움직이기 때문에 겉으로 보기에는 주황색 오브젝트의 월드 좌표가 움직이는 것을 확인할 수 있지만, 기존에 파란색 오브젝트의 하위로 들어가 있던 시점에서 보면, 파란색 오브젝트에 대하여 상대적인 위치는 변화하지 않았기 때문에 로컬 좌표계로 확인되는 현재로써는 결과적으로 변화가 없는 것으로 보이기 때문이다.
좌표 공간의 종류
렌더링 파이프라인에서는 로컬 스페이스에서 월드 스페이스, 카메라 스페이스, 클립 스페이스, 스크린 스페이스까지 총 4번의 공간 변환을 거친다.

최초로 오브젝트가 버텍스 셰이더에 들어올 때는 로컬 좌표계로 들어온다.
만약 어떤 박스 오브젝트가 한개 있다고 쳤을때, 그 오브젝트에 존재하는 총 8개의 버텍스들은 오브젝트 중심에서부터의 상대적인 위치를 각각 가지고 있다. 이것이 오브젝트 공간 기준인, 버텍스의 로컬 좌표이다.

그 다음 그 위치가 월드 좌표로 변환된다. (*사진의 모델 스페이스가 로컬 스페이스이다.)
여기서부터 MVP변환이 일어나는데 이는 각각 Model transformation, View transformation, Projection transformation를 묶어 부른 것이다.
엔진 내에서는 위와 같은 변환 과정들이 행렬을 곱하는 식으로 진행된다.
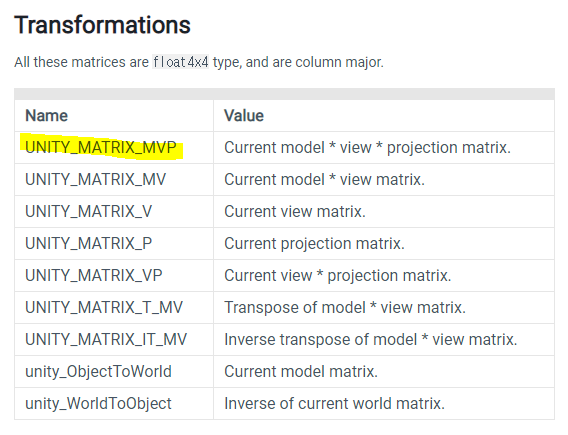
유니티 렌더 파이프라인에서 공간 변환시 사용되는 내장변수를 미리 만들어 두었다고 한다.
그렇다면 왜 여러 단계로 공간 변환을 거치는 것일까?
한 번에 최종 변환도 가능하지만, 다양한 목적의 셰이더 코드를 만들다보면 각각의 공간 좌표계가 필요할 때가 있다.
한 번에 변환을 가능하게 해주는 행렬이 바로 MVP 행렬이다.
https://docs.unity3d.com/Manual/SL-UnityShaderVariables.html
Unity - Manual: Built-in shader variables
Built-in shader helper functions Shader variants and keywords How do you use documentation throughout your workflow? Share your experience with us by taking this survey. Built-in shader variables Unity’s built-in include files contain global variables fo
docs.unity3d.com
■ 벡터
개념 이해
float3라는 변수는 3차원 공간 좌표를 한 번에 담을 수 있다. 예를 들어 (x,y,z)라는 공간 좌표가 있다고 치면 x.pos, y.pos, z.pos에 독립적으로 접근할 수 있게 된다. 이것이 3차원 벡터이다. 물론 이와 같이 2차원 좌표도 있을 수 있으며, 대표적으로는 uv가 있다. 이는 2차원 벡터이다.
이와 같이 하나의 공간 안에서, 원점을 기준으로 한 좌표를 벡터라고 한다. 화살표로 많이 표현된다. 즉, 원점에 대한 일종의 '방향'이라는 것이다.
따라서 벡터는 원점이 항상 기준점이 되기 때문에, 그래프 상에서
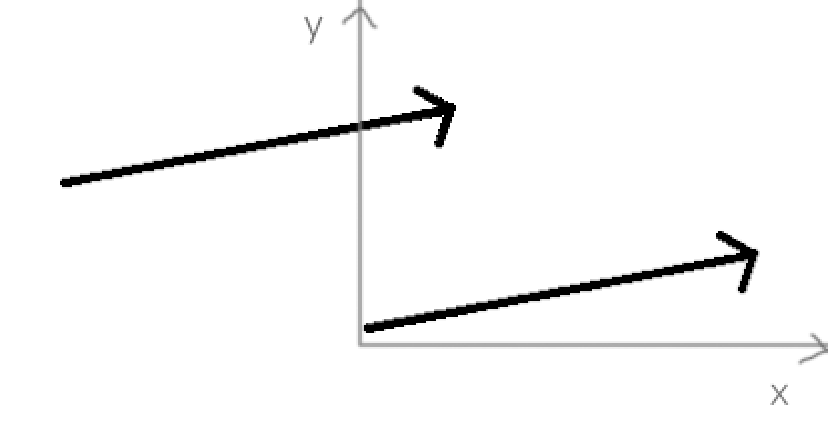
사진과 같은 두 개의 벡터가 있다고 해도, 벡터를 원점으로 옮겨보면 서로 같기 때문에 사진의 두 벡터는 같은 벡터라고 이야기된다.
이때, 위의 3차원 벡터 (x,y,z)에서 각각 하나의 요소들(x와 y와 z)을 1차원 스칼라라고 하며, 양 이라는 단어로 표현할 수 있다. 결과적으로 벡터는 1차원 스칼라가 확장된 개념이라고 볼 수 있다.
벡터의 덧셈
만약 (1,0)라는 벡터1이 있고 (1,0)라는 벡터2가 있다고 쳤을 때,
이 둘을 더하면 (1,1)이라는 벡터3이 된다.
쉽게 그림으로 표현하면 다음과 같다.

전부 원점 기준이다.
단위벡터
단위벡터란 길이가 1인 벡터이다.
만약 (1,1)인 벡터가 있다고 치면 원점으로부터의 순수한 거리는 1보다 클 것이다. length라는 함수가 있는데(hlsl에서 기본으로 제공해준다.) 만약 이 함수를 사용해서 (1,1)이라는 벡터의 길이를 구하면 1.xxx...라는 값으로 float 형태의 값을 리턴해줄 것이다.
위와는 다르게, 단위벡터는 무조건 길이가 1인 벡터를 뜻한다. (셰이더에서 많이 사용되는데, 여기에서 반지름 길이가 1이라는 것을 전제로 작동하는 삼각함수가 많이 사용되기 때문에 그렇다. 내적이라는 개념이 많이 사용되는 것 같다..)
단위벡터는 크기와 상관없이 방향을 정의하므로 유용하게 쓰인다.
정규화 (Normalize)
위에서 언급한 length 함수와 비교되는 normalize라는 함수가 있다. 이 함수는 위에서 float를 리턴해준 것과 다르게 벡터를 리턴해준다.
먼저 normalize라는 것은 우리말로 하면 '정규화'로써, 벡터의 크기(길이를 뜻한다)를 1로 만들어 단위 벡터가 되게 하는 것이다.
만약 normalize(1,1)과 같은 형태로 함수를 사용한다면, (1,1)벡터 위에서, 원점으로부터의 거리가 1인 점의 좌표를 리턴해주게 된다. 따라서 (0.7xxx,0.7xxx)와 같은 형태가 될 것이다.
이런 정규화 작업은, 벡터의 성분들 중에서 단순히 방향만 나타내고 싶을 때 주로 사용하게 된다.
청강문화산업대학교 3학년 1학기 게임그래픽엔진심화 수업 정리입니다.
'대학교 공부' 카테고리의 다른 글
| 엔진심화 10. 아웃라인 셰이더 (0) | 2021.06.09 |
|---|---|
| [엔진심화] 09. 구조체, 벡터 연산, 변환 행렬 (0) | 2021.06.02 |
| [엔진심화] 06. Z-Buffer, Render Queue (0) | 2021.05.05 |
| [엔진심화] 05. GlowDissolve, UV, Pixel Shader&Vertex Shader (0) | 2021.04.28 |
| [엔진심화] 04. SRP Batcher ,Keyword+ Shader graph Properties (0) | 2021.04.21 |




